Introduction: Equations can be thought of as powerful statements that convey information, much like sentences. In this blog post, we will delve into the world of linear equations, their significance, and how they can be used to solve systems of equations. Additionally, we will explore the concept of singularity in systems of linear equations and its implications. So, let's dive in!

Understanding Linear Equations: Linear equations resemble sentences, conveying information through mathematical statements. In the context of this post, we will focus on equations that involve numerical information. For example, the sentence "The price of an apple and a banana is $10" can be translated into the equation "a + b = 10," where 'a' represents the price of an apple and 'b' represents the price of a banana.
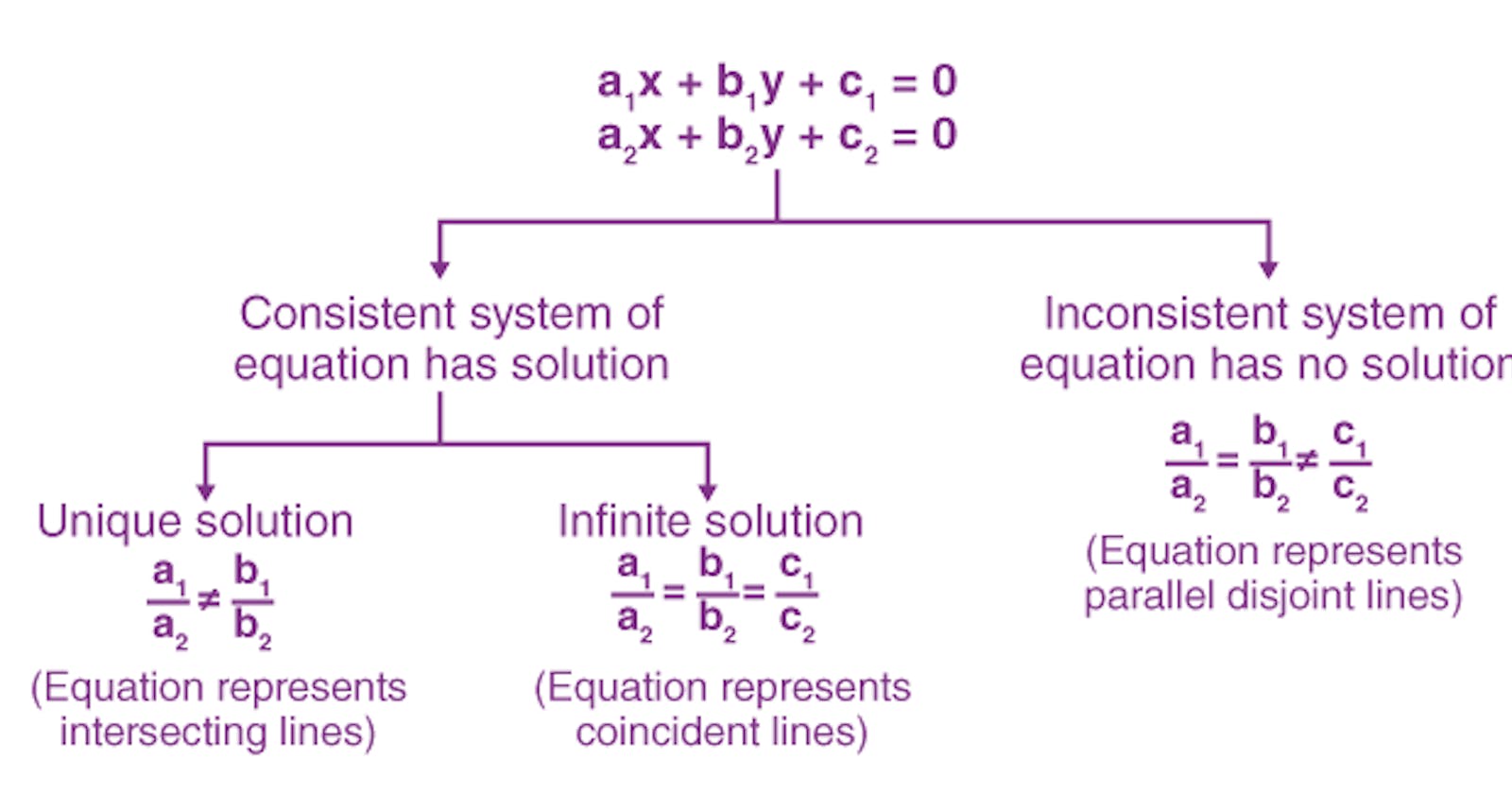
Solving Systems of Linear Equations: A system of linear equations involves multiple equations that share common variables. Just like sentences, systems of linear equations can be singular or non-singular, depending on the amount of information they provide. Solving these systems allows us to extract valuable insights.

System 1: Solving the First System of Linear Equations Let's consider a scenario where you visit a unique grocery store. The individual prices of items are unknown, and you only receive the total price at the register. By keeping track of different combinations, you aim to deduce the individual prices. On the first day, an apple and a banana cost $10, while on the second day, an apple and two bananas cost $12. By analyzing the difference in quantities and prices, we can conclude that apples cost $8, and bananas cost $2 each.
System 2: Not Enough Information In a similar scenario, on the first day, an apple and a banana cost $10, and on the second day, two apples and two bananas cost $20. However, these two equations are essentially the same, resulting in redundancy. This redundancy implies that we lack sufficient information to determine the exact prices. Hence, the system has infinitely many solutions, where any two numbers adding up to ten can be valid solutions.
System 3: Contradictory System Continuing the scenario, on the first day, an apple and a banana cost $10, and on the second day, two apples and two bananas cost $24. In this case, the equations contradict each other, indicating an error in the provided information. The system has no solutions as it is contradictory and singular.
Singular and Non-Singular Systems In summary, the first system of equations had a unique solution, indicating a non-singular system. The second system had infinitely many solutions due to redundancy, making it singular. Lastly, the third system lacked consistency, resulting in no solutions.

Linear Equations vs. Non-linear Equations: Linear equations follow a specific set of rules, allowing only scalar multiplication, addition, subtraction, and constant terms. Non-linear equations, on the other hand, encompass more complex mathematical functions such as squares, trigonometric functions, powers, and logarithms. Linear algebra, the study of linear equations, focuses on simpler equations that offer numerous manipulation and analysis possibilities.
Conclusion: Linear equations act as powerful tools to extract information from systems of equations. By understanding their properties and solving systems, we can deduce solutions, determine singularity, and recognize inconsistencies. Remember, linear algebra primarily deals with linear equations due to their simplicity and wide range of applications.