Introduction: Linear algebra is a fascinating field of mathematics that plays a crucial role in various scientific and engineering disciplines. At its core, linear algebra deals with systems of linear equations, which provide valuable insights into understanding relationships and solving problems. Before we dive into the world of equations, it is essential to grasp the language of mathematics. In this blog post, we will explore the concept of systems of sentences and how they relate to systems of equations, shedding light on their significance in the realm of linear algebra.
Sentences as Equations: When we think of equations, we often associate them with sentences conveying information about the world. In the context of systems of sentences, multiple sentences combine to provide a more comprehensive understanding, much like how equations combine to yield valuable insights. Let's consider an example involving animals and their colors to illustrate this concept further.
Suppose we have one dog and one cat, both of which have a single color. Our goal is to determine the color of each animal using systems of sentences. Let's examine three different systems to gain insights into their characteristics.
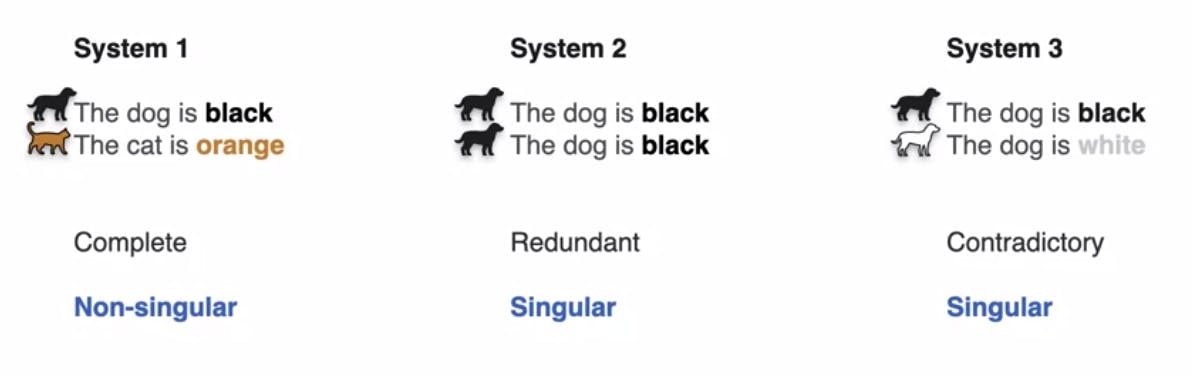
Complete System: System 1 consists of two sentences: "The dog is black" and "The cat is orange." Each sentence carries one piece of information, resulting in a complete system. A complete system has as many pieces of information as sentences, making it highly informative.
Redundant System: System 2 comprises two identical sentences: "The dog is black, and the dog is black." Although this system has two sentences, it conveys only one piece of information. Such systems are called redundant since the sentences repeat themselves.
Contradictory System: System 3 contains contradictory sentences: "The dog is black, and the dog is white." Since we have only one dog, it cannot possess both black and white colors simultaneously. Hence, this system is called contradictory.
Understanding System Characteristics: The informativeness of a system depends on the number of sentences it contains and whether they are redundant or contradictory. We introduce terminology that will be used throughout the course:
Non-Singular Systems: A non-singular system is complete, carrying as many pieces of information as sentences. It is the most informative type of system.
Singular Systems: Singular systems are either redundant or contradictory, conveying fewer pieces of information than the number of sentences they contain.
Systems of sentences can include more than two sentences; they can be as extensive as needed. Let's explore systems with three sentences to further illustrate their characteristics.

Example: Analyzing Three-Sentence Systems In this new example, we have three animals and want to determine their colors. Let's examine four systems:
Complete and Non-Singular System: System 1 consists of three different sentences: "The dog is black," "The cat is orange," and "The bird is red." Each sentence provides one unique piece of information, resulting in a complete and non-singular system.
Redundant and Singular System: System 2 has two sentences: "The dog is black, and the dog is black." As the first and second sentences convey the same information, this system is redundant and singular.
More Redundancy: System 3 includes three identical sentences: "The dog is black, the dog is black, and the dog is black." This system is highly redundant since all sentences express the same information.
Contradictory System: System 4 comprises three contradictory sentences: "The dog is black, the dog is white, and the bird is red." The contradictory nature of the sentences makes this system unable to convey accurate information.
Measure of Redundancy: The level of redundancy in a system can be measured using a mathematical concept called "rank," which will be explored later in the course.
Conclusion: Systems of sentences provide a valuable foundation for understanding systems of linear equations in linear algebra. By comparing them to sentences conveying information about the world, we gain insights into their characteristics, such as completeness, redundancy, and singularity. A complete system carries as much information as the number of sentences, while redundant and contradictory systems convey less information. Understanding these concepts is fundamental to solving real-world problems using linear algebra techniques.
